18. ročník, 1. série:
Petrovy prázdninové vzpomínky - řešení

1. Úloha

Šlo o šest věcí (dva stany, nářadí na opravy, lékárničku, vařič a hrnec). Kolika způsoby jsme je mohli rozdělit mezi nás čtyři, pokud každý měl vézt alespoň jednu věc?

Úlohu budeme řešit přiřazováním chlapců k věcem. Chlapce označíme čísly 0, 1, 2, 3. Lze snadno určit, kolik je všech možností rozdělení pro případ, kdy nejsou kladeny žádná další omezení. Každé z věcí lze přiřadit 4 chlapce, a proto možností je 4⁶ = 4096. Kdybychom tyto možnosti zapisovali pomocí čísel, byla by to všechna šestimístná čísla složená z číslic 0, 1, 2, 3.

Zadání však klade omezující podmínku, aby každý vezl alespoň jednu věc. Mohou tedy nastat 4 případy toho, kdy jeden z chlapců veze 3 věci, nebo 6 případů, kdy dva chlapci mají 2 věci.

1. Nejprve určíme počet možností pro případ, kdy jeden veze 3 věci, tj. hledáme šestimístná čísla, ve kterých se vyskytují 4 různé číslice a jedna z nich je obsažena právě třikrát.
   Hledejme např. čísla složená z 1, 2, 3 a třech 0. Čtveřice obsahující tři nuly a jedničku jsou 4. Přidáme-li k těmto čtveřicím pátou číslici (dvojku), získáme 5krát více čísel a přidáním další číslice (trojky) 6krát více čísel. Tedy šestimístných čísel složených z 1, 2, 3 a třech nul je 4 . 5 . 6 = 120.
   Počítali jsme čísla, ve kterých se opakují nuly. Mohli se však opakovat i čísla 1, 2 nebo 3 a proto všech možností, jak lze utvořit šestimístná čísla je 4 . 4 . 5 . 6 = 480.
2. Zadruhé určíme počet možností pro případ, kdy dva z chlapců vezou 2 věci, tj. hledáme šestimístná čísla, ve kterých se vyskytují 4 různé číslice a dvě z nich jsou obsaženy právě dvakrát.
   Hledejme například čísla složená z dvou 0 a dvou 1, 2 a 3. Čtyřmístná čísla obsahující dvě jedničky a dvě nuly lze utvořit 6 způsoby. Přidáme-li pátou číslici (dvojku), získáme 5krát více čísel a přidáním další číslice (trojky) 6krát více čísel. Tedy šestimístných čísel složených z 0, 0, 1, 1, 2, 3 je 6 . 5 . 6 = 180. Toto je jedno konkrétní řešení pro případ, kdy se opakují čísla 0 a 1. Mohli se však opakovat i jiné dvojice. Kombinací dvojic ze čtyř prvků je 6 a proto možností, jak utvořit šestimístná čísla je 6 . 6 . 5 . 6 = 1080.

Celkem tedy existuje 1560 různých možností rozdělení. Pro názornost uvádíme výčet generovaný počítačem.

2. Úloha

Urči poslední číslici a dvojčíslí čísla 4²⁰⁰⁴.

Úlohu můžeme například řešit tak, že vypíšeme poslední dvojčíslí několika prvních členů posloupnosti 4ⁿ ; nÎN: {04, 16, 64, 56, 24, 96, 84, 36, 44, 76, 04, 16...}.

V řádu jednotek se střídají čísla 4 a 6 a platí, že pro liché exponenty končí mocnina čtyřky číslem 4 a pro sudé exponenty číslem 6. Poslední dvojčíslí se opakuje s periodou délky 10.

Poslední číslice hledaného čísla je 6 a dvojčíslí 56.

3. Úloha

To je náhoda – ručičky (hodinová a minutová) se zrovna překrývají. Od 8 h ráno, kdy jsme vyjeli, je to už počtrnácté. Kolik je hodin?

K překrytí ručiček dochází 11krát za 12 h, tj. jednou za

K prvnímu překrytí došlo kolem 8.43 h a ke čtrnáctému asi ve 22.55 h.

4. Úloha

V jaké číselné soustavě platí rovnost 4 . 9 = 26?

Označíme základ neznámé soustavy písmenem z a rovnici přepíšeme:

4z⁰ . 9z⁰ = 2z¹ + 6z⁰

Upravíme na tvar 4 .9 = 2z + 6 a vypočítáme z = 15.

Rovnost platí v soustavě o základu patnáct.

5. Úloha

Nakreslete pomocí pravítka bez měřítka rovnoběžku s přímkou bodem, který na dané přímce neleží.

Omlouváme se, ale úloha byla zadána chybně a povolenými nástroji nelze řešit.
Konstrukci lze provést například pomocí pravítka s ryskou, užitím kružítka a pravítka, nebo rovnoběžnítkem (pravítko pro kreslení rovnoběžek). Tyto nástroje však nebyli povoleny a proto úlohu nelze vyřešit.

Správné zadání zní takto: Na přímce (a) jsou dány dva různé body (B, C) a jejich střed (D). Pomocí pravítka sestrojte rovnoběžku (g) bodem (A), který na dané přímce neleží.

Po stažení apletu (cca 1MB) se zobrazí animace vytvořená programem Cinderella.

6. Úloha

Lucii a Fandovi je dohromady 36 let. Fandovi je dvakrát víc, než bylo Lucce, když byl pětkrát mladší, než je dnes Lucka. Kolik let je Lucii?

Zadané údaje přehledně zaznamenáme do tabulky:

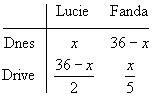
Protože víme, že rozdíl věků obou sourozenců je stálý, sestavíme na základě v tabulce uvedených údajů rovnici

která má řešení x = 20.

Lucii je dnes 20 let.