18. ročník

18. ročník, 3. série:
Petrovy prázdninové vzpomínky - řešení

1. úloha

Nakreslete jedenáct bodů tak, aby je šlo spojit jedenácti přímkami a na každé z těchto přímek ležely právě tři z těchto bodů.

Například:

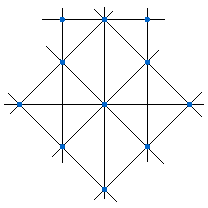
2. úloha

Fanda (F), Martina (Ma), Michal (Mi), Petr (P) a Tomáš (T) se vážili na vahách ve trojicích (F,Ma,Mi), (Ma,Mi,P), (Mi,P,T), (F,P,T), (F,Ma,T). Tyto trojice v uvedeném pořadí měli hmotnost postupně 176, 177, 185, 187 a 172 kg. Jaká byla hmotnost každého jednotlivce?

Ze zadaných údajů sestavíme rovnice:

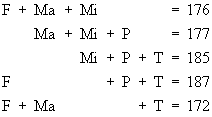
Utvoříme součet rovnic:

a vyjádříme jednotlivé neznámé:

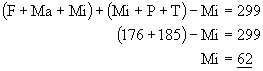
Obdobně použijeme rovnice:

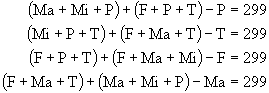
Fanda vážil 64 kg, Michal 62 kg, Petr 65 kg, Tomáš 58 kg a Martina vážila 50 kg.

3. úloha

Martina se vozí na řetízkovém kolotoči. Tomáš, který se na kolotoč bojí, obíhá pod kolotočem po kružnici. Když běží po směru otáčení, míjí se s Martinou každých 15 sekund. Běží-li proti směru otáčení, potkají se každých 10 sekund. Jak dlouho trvá jedna otáčka kolotoče?

Označme vM, vT rychlosti Martiny a Tomáše. Obvod kruhu při souhlasném pohybu obou je vM . 15 - vT . 15, při opačném pohybu vM . 10 + vT . 10. Odsud vM = vT . 5. Jedna otáčka kolotoče tedy trvá

.

4. úloha

Nechť dáma stojí (kdekoli) na prázdné šachovnici. Kolik celkem různých tahů může udělat?

Do každého pole šachovnice napíšeme číslo, které udává, kolik tahů z něho může dáma udělat. Dostaneme toto čtvercové schéma:

21 21 21 21 21 21 21 21
21 23 23 23 23 23 23 21
21 23 25 25 25 25 23 21
21 23 25 27 27 25 23 21
21 23 25 27 27 25 23 21
21 23 25 25 25 25 23 21
21 23 23 23 23 23 23 21
21 21 21 21 21 21 21 21

Hledaný počet tahů je součtem všech čísel v tomto schématu, tj. číslem

5. úloha

V automatu zbylo 20 žvýkaček různých příchutí. Jedna z nich byla citrónová a nikdo z nás ji nechtěl. Jaká je pravděpodobnost, že každému z nás pěti vydá automat jinou než citrónovou?

Pro pravděpodobnost P platí:

Pravděpodobnost uvedeného jevu je 75procentní.

6. úloha

Prázdniny se krátí. Do jejich konce zbývá ještě tolik dní, kolik je šesticiferných čísel dělitelných číslem 60 a obsahujících pouze cifry 0, 1, 2. Kolik dnů zbývá?

Hledaná čísla končí 0, mají ciferný součet [CS] dělitelný třemi a poslední dvojčíslí dělitelné čtyřmi.

Čísla tvaru: 1xxx00 Čísla tvaru: 2xxx00
CS Místo „x“ ∑ CS Místo „x“ ∑
3 0,1,1 3 3 0,0,1 3
3 0,0,2 3 6 1,1,2 3
6 1,2,2 3 6 0,2,2 3
Čísla tvaru: 1xxx20 Čísla tvaru: 2xxx20
CS Místo „x“ ∑ CS Místo „x“ ∑
3 0,0,0 1 6 0,1,1 3
6 0,1,2 6 6 0,0,2 3
6 1,1,1 1 9 1,2,2 3
9 2,2,2 1      

Celkem tedy existuje 36 možností a do konce prázdnin zbývá 36 dnů.

Podporujeme:

Pikomat na TOPlistu